[PDF] Trigonometry Formula in Hindi|त्रिकोणमिति सूत्र हिंदी में
Trigonometry Formula in Hindi त्रिकोणमिति सूत्र SSC, NDA, CDS तथा अन्य प्रतियोगी परीक्षाओं की दृष्टि से महत्वपूर्ण स्थान रखता है। यदि हम विगत तीन या चार वर्षों के SSC तथा अन्य प्रतियोगी परीक्षाओं के प्रश्न-पत्रों का विश्लेषण करें, तो हमें ज्ञात होता है कि त्रिकोणमिति से SSC (10+2 स्तर, स्नातक स्तर व CPO) तथा अन्य प्रतियोगी परीक्षाओं में तीन से चार प्रश्न पूछे जा रहे हैं।
- कोण मापन की पद्धतियाँ (System of Measurement of an Angle)
- समकोण त्रिभुज में लम्ब, आधार तथा कर्ण
- पाइथागोरस प्रमेय (Pythagorus Theorem)
- त्रिकोणमितीय अनुपात (Trigonometric Ratio)
- Relations between Trigonometric Ratios
- त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities)
- Trigonometry: Maximum & Minimum Value
- Important Results for Trigonometry
त्रिकोणमिति Trigonometry Formula का शाब्दिक अर्थ है त्रिभुज की भुजाओं और कोणों से सम्बन्धित माप |
![[PDF] Trigonometry Formula in Hindi | त्रिकोणमिति सूत्र हिंदी में](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh41RfMwps-Z5YzEOlFhyw52rDTC7iEyYpucgRSeYL9734vPQ_sL3iQHA0-iU4SEoHbVdjyWO-TWIb8PHQulFszXbgqIseVg_u2z0DR9uJFZ1-TQDHr9GwnEgWpquCDBZQTr3SEOstnOw4/s800/Trigonometry+Formula+in+Hindi.png "[PDF] Trigonometry Formula in Hindi | त्रिकोणमिति सूत्र हिंदी में")
आधुनिक गणित में त्रिकोणमिति Trigonometry Formula का मुख्य कार्य त्रिभुज की भुजाओं को नापना एवं भुजाओं व कोणों के मध्य पारस्परिक सम्बन्ध स्थापित करना है। त्रिकोणमितीय अनुपात, सर्वसमिका तथा ऊँचाई एवं दूरी से सम्बन्धित प्रश्नों को हल करने में त्रिभुज की भुजाओं तथा कोणों के पारस्परिक सम्बन्धों का प्रयोग किया जाता है।
मानचित्रों को बनाने में समस्त तल को त्रिभुजों में विभाजित कर दिया जाता है तथा त्रिकोणमितीय अनुपात व सर्वसमिकाओं की सहायता से विभिन्न स्थानों की ऊँचाइयाँ तथा दूरियाँ ज्ञात कर ली जाती हैं।
त्रिकोणमिति में विभिन्न स्थानों की ऊँचाई तथा दूरी ज्ञात करने में मुख्य रूप से समकोण त्रिभुज का प्रयोग किया जाता हैं। यदि किसी समकोण त्रिभुज की कुछ भुजाएँ और कोण ज्ञात हो, तो शेष भुजाओं और कोणों को त्रिकोणमितीय अनुपात व त्रिकोणमितीय सर्वसमिकाओं की सहायता से ज्ञात किया जा सकता है।
Read Also : [PDF] बीजगणित के सूत्र | Algebra Formulas Hindi
Mensuration Formula In Hindi | मेंसुरेशन फॉर्मूला हिंदी में
कोण मापन की पद्धतियाँ (System of Measurement of an Angle)
कोणों को मापने की निम्न तीन पद्धतियाँ हैं
1. षाष्टिक पद्धति (Sexagesimal System)
इस पद्धति में कोणों को अंश में मापा जाता है तथा अंश (°) मिनट (') तथा सेकण्ड ('') में निम्न सम्बन्ध होता है
1 समकोण = 90° (90° अंश)
1° = 60' (60 मिनट) तथा 1' = 60'' (60 सेकण्ड)
2.शतिक पद्धति (Centesimal System)
इस पद्धति में कोणों को ग्रेड में मापा जाता है तथा ग्रेड (g), मिनट (') और सेकण्ड ('') में निम्न सम्बन्ध होता है
1 समकोण 100 ग्रेड (100 g)
1g = 100' (100 मिनट) तथा 1' = 100'' (100 सेकण्ड)
3. वृत्तीय पद्धति (Circular Measure)
इस पद्धति में कोणों को रेडियन में मापा जाता है। एक रेडियन वह कोण है जो किसी वृत्त की त्रिज्या के बराबर लम्बाई के चाप द्वारा उस वृत्त के केन्द्र पर अन्तरित किया जाता है तथा इसे 1c से निरूपित करते हैं।
यदि किसी वृत्त के चाप की लम्बाई l व त्रिज्या r तथा केन्द्र पर बना कोण θ हो, तब
कोण = चाप / त्रिज्या अर्थात् θ = l/r
महत्वपूर्ण तथ्य
πc = 1 रेडियन = ( 180/π)° = 57°16’22’’
किसी कोण की माप को अंश (डिग्री) से रेडियन में बदलना हो, तो माप में π/180° से गुणा करते हैं।
किसी कोण की माप को रेडियन से अंश में बदलना हो, तो माप में 180°/π से गुणा करते हैं अथवा π के स्थान पर 180° रखकर हल करते हैं।
समकोण त्रिभुज में लम्ब, आधार तथा कर्ण
(Base, Perpendicular and Hypotenuse in Right Angle Triangle)
किसी समकोण त्रिभुज में न्यून कोण के सामने वाली भुजा लम्ब, संलग्न भुजा आधार तथा समकोण के सामने वाली भुजा को कर्ण कहा जाता है।
पाइथागोरस प्रमेय (Pythagorus Theorem)
पाइथागोरस प्रमेय के अनुसार, समकोण △ABC में, (कर्ण)2 = (आधार)2 + (लम्ब)2
कर्ण = AC. आधार = AB तथा लम्ब = BC
(AC)2 = (AB)2 + (BC)2
AC = √(AB)2 + (BC)2
त्रिकोणमितीय अनुपात (Trigonometric Ratio)
एक समकोण त्रिभुज के न्यून कोणों के सापेक्ष, त्रिभुज की भुजाओं के अनुपात को त्रिकोणमितीय अनुपात कहते हैं। त्रिकोणमितीय अनुपात छः प्रकार के होते हैं जिन्हें निम्न प्रकार से परिभाषित किया जा सकता है।
△ABC एक समकोण त्रिभुज है जिसमें AB आधार, AC लम्ब तथा BC कर्ण है, तब
Relations between Trigonometric Ratios
sin θ = लम्ब / कर्ण = 1/cosec θ
cos θ = आधार / कर्ण = 1/ sec θ
tan θ = लम्ब / आधार = 1/cot θ = sin θ / cos θ
cosec θ = कर्ण / लम्ब = 1/sin θ
sec θ = कर्ण / आधार = 1/cos θ
cot θ = आधार / लम्ब = 1/tan θ = cos θ / sin θ
त्रिकोणमितीय सर्वसमिकाएँ (Trigonometric Identities)
त्रिकोणमितीय अनुपातों से बनी समीकरण जो θ के सभी मानों के लिए सत्य होती है, त्रिकोणमितीय सर्वसमिकाएँ कहलाती हैं |
(i) sin2 θ + cos2 θ = 1
(ii) 1 + tan2 θ = sec2 θ
(iii) 1 + cot2 θ = cosec2 θ
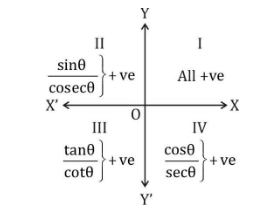
Value of Trigonometric Ratios in Different Quadrants
Different Values of Specific Angle of Trigonometric Ratio
कोण 0°, 30°, 45°, 60°, 90° के त्रिकोणमितीय अनुपात के आधार पर प्रश्न को हल करने के लिए आपको निम्न तालिका याद करनी चाहिए
Relation Between Square Of Different Types Of Trigonometric ratios
Important Concept to Solve a Specific Type of Question
यदि A + B = 90°
यह हमेशा सत्य होंगे:
(i) sin A. sec B = 1 or sin A = cos B
(ii) cos A. cosec B = 1 or sec A = cosec B
(iii) tan A. tan B = 1 or tan A = cot B
(iv) cot A. cot B = 1
(v) sin²A + sin² B = 1
(vi) cos² A + cos² B = 1
Important Formula for Sum and Difference Of Two Angles
(1) sin (A+B) =sinA. cosB + cosA sinB
(2) sin(A - B) =sinA. cosB - cosA sinB
(3) cos(A+B) =cosA. cosB - sinA sinB
(4) cos(A-B) = cosA. cosB+sinA sinB
(6) 2 cosA. sinB = sin(A+B)-sin (A-B)
(7) 2 sinA. sinB = cos(A-B)-cos(A+B)
(8) 2 cosA.cosB = cos(A+B)+cos(A-B)
(9) sin²A-sin²B = sin(A+B). sin(A-B)
(10) cos²A-cos²B = cos(A+B).cos (A-B)
Different Formula For Tangent
Important Results for Trigonometry
- यदि A + B + C = 180°
तो, tan A + tan B + tan C = tan A. tan B. tan C
- यदि A + B + C = 90°
तो, cot A + cot B + cot C = cot A cot B cot C
- यदि (a) sin θ + cosec θ = 2
