Mensuration all formula in hindi | क्षेत्रमिति के सभी फार्मूला हिंदी

  क्षेत्रमिति के सभी फार्मूला हिंदी | Mensuration all Formula in Hindi

क्षेत्रमिति फार्मूला (Mensuration all formula in Hindi) गणित की वह शाखा है जो ज्यामिति के विभिन्न आकृतियों mensuration all formula for class 8th/ mensuration formula for class 10thऔर (shape formula)आकृतियों के मापन से संबंधित है।

इसमें आकृतियों के क्षेत्रफल फार्मूला, आयतन फार्मूला आदि की गणना शामिल है। विभिन्न क्षेत्रमिति (Mensuration) सूत्र परीक्षा बिंदु के लिए उपयोगी ज्यामिति में शामिल हैं।

Contents

1. 2D और 3D आकार क्या हैं?
2. 3D आकृतियों का क्षेत्रमिति सूत्र
3. वर्ग
4. आयत
5. समलम्ब चतुर्भुज
6. सम चतुर्भुज
7. बहुभुज
8. वृत्त
9. त्रिज्याखण्ड एवं वृत्तखंड
10. घन
11. घनाभ
12. बेलन (Roller)
13. शंकु
14. गोला
15. समबाहु त्रिभुज

इसमें आकृतियों के क्षेत्रफल, आयतन आदि की गणना शामिल है। विभिन्न क्षेत्रमिति फार्मूला(Mensuration formula) सूत्र परीक्षा बिंदु के लिए उपयोगी ज्यामिति में शामिल हैं।

इस विषय में उत्कृष्टता प्राप्त करने के लिए, आपको प्रश्नों को हल करने के लिए उपयोग किए जाने वाले सूत्रों और अवधारणाओं को जानना होगा। उचित स्पष्टीकरण के साथ इस पोस्ट में शामिल महत्वपूर्ण बुनियादी गणित क्षेत्रमिति फ़ार्मुलों की जाँच करें।

You can also read this

• Mensuration formula in hindi
• Current Affairs
• Uttarakhand gk notes
• Integration Formula
• Number system
• Algebra Formula
• Tense in hindi

क्या आपने कभी सोचा है कि आपकी कार को कितनी पार्किंग की जगह चाहिए? या आपके कमरे में किस आयाम का बिस्तर फिट हो सकता है? इन सवालों का जवाब क्षेत्रमिति सूत्रों में है। लैटिन में, क्षेत्रमिति का अर्थ है माप। इसलिए, क्षेत्रमिति गणित की वह शाखा है जो 2D और 3D ज्यामितीय आकृतियों की लंबाई, क्षेत्रफल और आयतन की गणना से संबंधित है। लेकिन अब आपको इन सूत्रों को सीखने की जरूरत क्यों है? जीआरई, जीमैट, एसएससी, आरबीआई ग्रेड बी, आदि जैसे परीक्षाओं के मात्रात्मक तर्क खंड को सबसे कठिन लेकिन उच्च स्कोरिंग खंड में से एक माना जाता है। इस प्रकार, गति और सटीकता अच्छा स्कोर करने में महत्वपूर्ण भूमिका निभाते हैं। अब यहाँ मासिक धर्म के सूत्रों को याद रखने की भूमिका आती है। यदि आप एक सूत्र याद कर सकते हैं, तो आप अन्य प्रश्नों पर अधिक समय लगा सकते हैं। यहां एक ब्लॉग है जो प्रतियोगी परीक्षाओं के लिए सभी प्रासंगिक क्षेत्रमिति फ़ार्मुलों को संकलित करता है।

मेंसुरेशन क्या है?

क्षेत्रमिति गणित की एक प्रमुख अवधारणा है और विभिन्न ज्यामितीय आकृतियों और आकृतियों के माप का अध्ययन करती है। जैसा कि चर्चा की गई है, कई प्रतियोगी परीक्षाओं में क्षेत्रमिति के सूत्र काम आते हैं। यह हमें विभिन्न 2-आयामी और 3-आयामी वस्तुओं के आयामों को समझने में मदद करता है। जबकि एक 2D आकृति में केवल दो आयाम होते हैं यानी लंबाई और चौड़ाई, एक 3D आकृति में लंबाई, चौड़ाई और ऊंचाई होती है। क्षेत्र (ए) और परिधि (पी) दो सामान्य पैरामीटर हैं जिन्हें हम 2 डी आकृतियों के लिए मापते हैं। 3डी के लिए, वॉल्यूम (वी), कुल, पार्श्व और घुमावदार सतह क्षेत्र की गणना की जाती है।

Shape	Volume (Cubic units)	Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units)	Total Surface Area (TSA) (Square units)
Cube	a³	4 a²	6 a²
Cuboid	l × b × h	2 h (l + b)	2 (lb +bh +hl)
Sphere	(4/3) π r³	4 π r²	4 π r²
Hemisphere	(⅔) π r³	2 π r²	3 π r²
Cylinder	π r² h	2π r h	2πrh + 2πr²
Cone	(⅓) π r² h	π r l	πr (r + l)

2D और 3D आकार क्या हैं?

2D आकृतियाँ- ज्यामिति में, द्वि-आयामी आकृति एक समतल समतल आकृति या एक आकृति होती है जिसमें केवल दो आयाम होते हैं अर्थात लंबाई और चौड़ाई। द्वि-आयामी या 2-डी आकृतियों में कोई मोटाई नहीं होती है और इसे केवल दो चेहरों में मापा जा सकता है। केवल 2D आकृतियों के क्षेत्रफल और परिधि की गणना की जा सकती है।

3डी आकार- एक त्रि-आयामी आकृति वह होती है जहां आकृति के तीन आयाम होते हैं अर्थात् लंबाई, चौड़ाई और मोटाई। हम आयतन, घुमावदार सतह क्षेत्र, 3D आकृतियों के कुल सतह क्षेत्र की गणना करते हैं।

Shape(आकार)	Area (क्षेत्रफल)	Perimeter (परिमाप)
वर्ग (Square)	a2	4a
आयत (Rectangle)	l * b	2(l + b)
वृत्त (Circle)	πr²	2πr
विषमबाहु त्रिकोण (Scalene Tringle)	√[s(s−a)(s−b)(s−c)], जहाँ, s = ( a + b + c )/2	a + b + c
(समद्विबाहु)Isosceles	½ * b * h	2a + b
Equilateral tringle	(√3/4) × a²	3a
समकोण त्रिभुज(Right Angle Tringle)	½ * b * h	b + कर्ण + h
विषमकोण(Rhombus)	½ * d1 * d2	4 * साइड
चतुर्भुज(Parallelogram)	b * h	2(l + b)
समलम्ब(Trapezium)	½ h (a + b)	a + b + c + d

Terms	Abbreviation(संक्षिप्त)	Unit(इकाई)	Definition(परिभाषा)
Area (क्षेत्र)	A	m2 or cm2	क्षेत्र वह सतह है जो बंद आकार से ढकी होती है।
Perimeter(परिमाप)	P	CM OR M	दी गई आकृति की सीमा के अनुदिश सतत रेखा की माप को परिमाप
Volume (आयतन)	V	cm3 or m3	एक 3D आकार द्वारा कब्जा किए गए स्थान को वॉल्यूम कहा जाता
Curved Surface Area (घुमावदार सतह क्षेत्र)	CSA	m2 or cm2	यदि कोई घुमावदार सतह है, तो कुल क्षेत्रफल को वक्र सतह क्षेत्र
Lateral Surface area (पार्श्व सतह क्षेत्र)	LSA	m2 or cm2	दी गई आकृति को घेरने वाली सभी पार्श्व सतहों का कुल क्षेत्रफल
Total Surface Area (कुल सतह क्षेत्रफल)	TSA	m2 or cm2	सभी घुमावदार और पार्श्व सतह क्षेत्रों के योग को कुल सतह क्षेत्र

 Mensuration formula in hindi | क्षेत्रमिति सूत्र  Hindi में 

3D आकृतियों का क्षेत्रमिति Mensuration formula सूत्र-

Shape(आकार)	Volume	Curved Surface Area	Total Surface Area
घनक्षेत्र (Cube)	a3	4a2	6a2
घनाभ (Cuboid)	L * b* h	2h(l + b)	2( lb + bh + hl)
क्षेत्र (Sphere)	(4/3) πr3	4 πr²	4 πr²
गोलार्द्ध (Hemisphere)	(2/3) Πr3	2 πr²	3 πr²
सिलेंडर (Cylinder)	πr²h	2 πrh	2 πrh + 2 πr²
शंकु (Cone)	(1/3)πr²h	Πrl	Πr (r + l)

 वर्ग :-

एक वर्ग में 4 भुजाएँ और 4 शीर्ष होते हैं।एक वर्ग की सभी भुजाओं की लंबाई बराबर होती है।सभी आंतरिक कोण समान और समकोण हैं।सभी आंतरिक कोणों का योग 360° होता है।

• वर्ग की परिमाप = 4 × a
• वर्ग का क्षेत्रफल = (भुजा × भुजा) = a²
• एवं भुजा = √ क्षेत्रफल
• वर्ग का क्षेत्रफल = ½ × (विकर्णो का गुणनफल) = ½ × d2
• वर्ग का विकर्ण = एक भुजा × √2 = a × √2
• वर्ग का विकर्ण = √2 × वर्ग का क्षेत्रफल

आयत :-

एक  में 4 भुजाएँ और 4 शीर्ष होते हैं।एक वर्ग की आमने- सामने की भुजाएं बराबर होती है।सभी आंतरिक कोण समान और समकोण हैं। सभी आंतरिक कोणों का योग 360° होता है।

• आयत का परिमाप = 2(लम्बाई + चौड़ाई)
• आयत का क्षेत्रफल = लंबाई ×चौड़ाई
• आयत का विकर्ण =√(लंबाई² + चौड़ाई²)

समलम्ब चतुर्भुज :-

एक समलम्ब चतुर्भुज एक समांतर चतुर्भुज है यदि इसके विपरीत पक्षों के दोनों जोड़े समानांतर हैं।एक समलम्ब चतुर्भुज एक वर्ग है यदि इसके विपरीत पक्षों के दोनों जोड़े समानांतर हैं; इसकी सभी भुजाएँ समान लंबाई की हैं और एक दूसरे से समकोण पर हैं।

एक समलम्ब चतुर्भुज एक आयत हो सकता है यदि इसके विपरीत पक्षों के दोनों जोड़े समानांतर हों; इसकी सम्मुख भुजाएँ समान लंबाई की हैं और एक दूसरे से समकोण पर हैं।

समलम्ब चतुर्भुज का क्षेत्रफल

• = ½ (समान्तर भुजाओं का योग x ऊंचाई)
• = ½ (समान्तर चतुर्भुज का क्षेत्रफल)
• = ½ (आधार x संगत ऊंचाई)

परिमाप, P = a + b+ c + d

क्षेत्रमिति के सभी फार्मूला हिंदी | Mensuration formula in hindi

सम चतुर्भुज  :-

समचतुर्भुज एक विशेष प्रकार का समांतर चतुर्भुज है जिसकी सभी भुजाएँ बराबर होती हैं।एक वर्ग और समचतुर्भुज के बीच का अंतर यह है कि एक वर्ग के सभी कोण समकोण होते हैं, लेकिन एक समचतुर्भुज के कोण समकोण होने की आवश्यकता नहीं है।तो, समकोण वाला एक समचतुर्भुज एक वर्ग बन जाता है।

हम कह सकते हैं, "हर वर्ग समचतुर्भुज है लेकिन सभी समचतुर्भुज वर्ग नहीं हैं।"

∠A + ∠B + ∠C + ∠D = 360°

• विषमकोण चतुर्भुज का क्षेत्रफल = ½ × दोनों विकर्णो का गुणनफल
• अर्थात, A = (d1 × d2)/2 वर्ग इकाई
• समचतुर्भुज की परिमाप = 4 × एक भुजा
• समचतुर्भुज में = (AC)² + (BD)² = 4a²
• चक्रीय चतुर्भुज का फार्मूला

1. ∠A + ∠C = 180°
2. ∠B + ∠D = 180°

• क्षेत्रफल = √[s(s-a) (s-b) (s – c) (s – c)]
• परिमाप, S = ½ ( a + b + c + d )

बहुभुज:-

• n भुजा वाले चतुर्भुज का अन्तः कोणों का योग = 2(n -2) × 90°
• समबहुभुज के प्रत्येक अंतः कोण = (n – 2) / 2 × 180°
• n भुजा वाले बहुभुज के बहिष्कोणों का योग = 360°
• बहुभुज के कुछ अंतः कोणों का योग = (n – 2) × 180°
• n भुजा वाले समबहुभुज का प्रत्येक अन्तः कोण = [2(n – 2) × 90°] / n
• बहुभुज की परिमिति = n × एक भुजा
• नियमित षट्भुज का क्षेत्रफल = 6 × ¼√3 (भुजा)²
• n भुजा वाले समबहुभुज का प्रत्येक भहिष्यकोण = 360°/n
• नियमित षट्भुज का क्षेत्रफल = 3√3×½ (भुजा)²
• समषट्भुज की भुजा = परिवृत की त्रिज्या
• नियमित षट्भुज की परिमति = 6 × भुजा
• n भुजा वाले नियमित बहुभुज के विकर्णो की संख्या = n(n – 3)/2

वृत्त :- 

एक वृत्त एक बंद आकार है जो एक बिंदु को ट्रेस करके बनता है जो एक विमान में चलता है जैसे कि किसी दिए गए बिंदु से इसकी दूरी स्थिर होती है। सर्कल शब्द ग्रीक शब्द किर्कोस से लिया गया है, जिसका अर्थ है घेरा या अंगूठी। इस लेख में, हम मंडलियों, उनके गुणों और विभिन्न वृत्त सूत्रों से संबंधित महत्वपूर्ण शब्दों को शामिल करते हैं।

• वृत्त का क्षेत्रफल = πr²
• वृत्त का व्यास = 2r
• वृत्त की परिधि = 2πr
• वृत्त की परिधि = πd
• वृत्त की त्रिज्या = √व्रत का क्षेत्रफल/π
• वृताकार वलय का क्षेत्रफल = π (R2 – r2)
• अर्द्धवृत्त की परिधि = ( π r  + 2 r )
• अर्द्धवृत्त का क्षेत्रफल = 1/2πr²

त्रिज्याखण्ड एवं वृत्तखंड का फार्मूला

• त्रिज्याखण्ड का क्षेत्रफल = θ/360° × πr²
• चाप की लम्बाई = θ/360° × 2πr
• त्रिज्याखण्ड की परिमिति = 2r + πrθ/180°
• वृतखण्ड का क्षेत्रफल = (πθ/360° – 1/2 sinθ)r²
• वृतखण्ड की परिमिति = (L + πrθ)/180° , जहाँ L = जीवा की लम्बाई

घन :-

 घन एक 3-डी . होता है ठोस आकार, जिसमें 6 चेहरे हैं। घन त्रि-आयामी अंतरिक्ष में सबसे सरल आकृतियों में से एक है। एक घन के सभी छह फलक वर्गाकार होते हैं, एक द्वि-आयामी आकृति।

• घन का आयतन = भुजा × भुजा × भुजा = a3
• घन का परिमाप = 4 a²
• पार्श्वपृष्ठ का एक किनारा = √ ( पार्श्वपृष्ठ का क्षेत्रफल / 4 )
• घन का एक किनारा = 3√आयतन
• घन का एक किनारा = √ (सम्पूर्ण पृष्ठ का क्षेत्रफल / 6 )
• घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a²
• घन का विकर्ण = √3 × भुजा

घनाभ :- 

घनाभ भी एक बहुफलक है जिसमें छह फलक, आठ शीर्ष और बारह किनारे होते हैं। घनाभ के फलक समानांतर होते हैं। लेकिन घनाभ के सभी फलक विमाओं में समान नहीं होते हैं

• घनाभ का आयतन =  l × b × h
• घनाभ का परिमाप = 2(l + b) × h
• घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
• घनाभ का विकर्ण = √(l² + b² + h²)
• घनाभ की ऊँचाई = आयतन / ( लम्बाई × चौड़ाई )
• घनाभ की चौड़ाई = आयतन / ( लम्बाई × ऊँचाई )
• कमरें के चारों दीवारों का क्षेत्रफल = 2h ( l + b )
• ढक्कनरहित टंकी का क्षेत्रफल = 2h ( l + b ) + lb
• छत या फर्श का क्षेत्रफल = लम्बाई × चौड़ाई

बेलन (Roller) :-

• बेलन का आयतन = πr²h
• बेलन की ऊँचाई = आयतन / πr²
• लम्बवृतीय बेलन की त्रिज्या = √ ( आयतन / πh)
• खोखले बेलन में लगीधातु का आयतन = πh (R² – r² )
• बेलन का वक्रपृष्ठ का क्षेत्रफल = 2πrh
• बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr ( h + r )
• लम्बवृतीय बेलन की ऊँचाई = (बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल / 2πr) – r
• लम्बवृतीय बेलन का आधार का क्षेत्रफल =  πr²

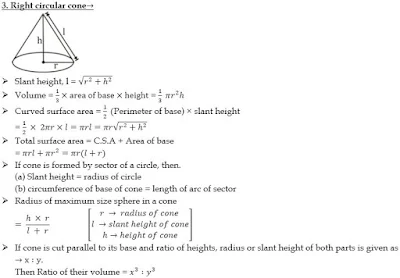
शंकु :-

एक शंकु एक आकृति है जो रेखा खंडों या रेखाओं के एक सेट का उपयोग करके बनाई जाती है जो एक सामान्य बिंदु को जोड़ती है, जिसे शीर्ष या शीर्ष कहा जाता है, एक गोलाकार आधार के सभी बिंदुओं (जिसमें शीर्ष नहीं होता है)। शंकु के शीर्ष से आधार तक की दूरी शंकु की ऊंचाई है। वृत्ताकार आधार ने त्रिज्या का मान मापा है। और आधार की परिधि पर शीर्ष से किसी भी बिंदु तक शंकु की लंबाई तिरछी ऊंचाई है। इन राशियों के आधार पर शंकु के पृष्ठीय क्षेत्रफल और आयतन के लिए सूत्र प्राप्त होते हैं। आकृति में आप देखेंगे कि शंकु जो इसकी ऊँचाई, उसके आधार की त्रिज्या और तिरछी ऊँचाई से परिभाषित होता है।

• शंकु का आयतन = 1/3 πr²h
• लम्बवृतीय शंकु की तिर्यक ऊँचाई = √ ( h2 + r2 )
• शंकु की ऊँचाई = √ (l2 – r2 )
• शंकु की आधार की त्रिज्या = √ (l2 – h2 )
• शंकु के वक्र पृष्ठ का क्षेत्रफल = πrl
• लम्बवृतीय शंकु के सम्पूर्ण पृष्ठ का क्षेत्रफल = πr ( l + r )
• शंकु का आधार का क्षेत्रफल = πr²

गोला:-

वृत्त एक बंद द्विविमीय आकृति है जिसमें तल के सभी बिंदुओं का समुच्चय किसी दिए गए बिंदु से समान दूरी पर होता है जिसे "केंद्र" कहा जाता है। वृत्त से गुजरने वाली प्रत्येक रेखा परावर्तन समरूपता की रेखा बनाती है।

• गोले का वक्रपृष्ठ का क्षेत्रफल = 4πr²
• गोला का आयतन = 4/3 πr³
• गोलीय शेल का आयतन = 4/3 π ( R³ – r³ )
• गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल = 4/3 π ( R² – r² )
• घन ने सबसे बड़े गोले का आयतन = 1/6 a³
• घन में सबसे बड़े गोले का पृष्ठ क्षेत्रफल = πa²
• गोले में सबसे बड़े घन की एक भुजा = 2R / √3
• अर्द्ध गोला के वक्रपृष्ठ का क्षेत्रफल = 2 πr²
• किसी अर्द्ध गोला के सम्पूर्ण पृष्ठ का क्षेत्रफल = 3 πr²
• अर्द्ध गोला का आयतन = 2/3 πr³

समबाहु त्रिभुज :-

• समबाहु त्रिभुजा का क्षेत्रफल = (√3)/4 × भुजा2
• समबाहु त्रिभुज का शीर्षलम्ब = (√3)/4 × भुजा
• परिमाप = 3 × भुजा

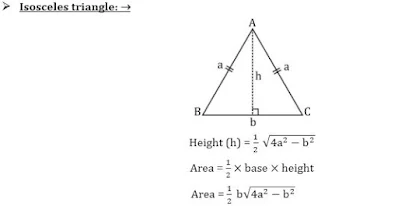
समद्विबाहु त्रिभुज का सूत्र

• समद्विबाहु त्रिभुज का क्षेत्रफल, A = a / 4 b √ (4b² – a²)
• समद्विबाहु त्रिभुज का शीर्षलम्ब = a / 4 b √ (4b² – a²)
• परिमाप,  P = 2a + b

विषमबहु त्रिभुज

• विषमबहु त्रिभुज का क्षेत्रफल, A =√ [ s(s – a)(s – b)(s – c) ]
• दुसरें रूप में, A = ½ × आधार × ऊँचाई
• अर्धपरिधि P = ½ ( a + b + c )

समकोण त्रिभुज

• समकोण त्रिभुज का क्षेत्रफल,  A = ½ × आधार × ऊँचाई
• समकोण समद्विबाहु त्रिभुज का परिमाप = (2 + √2) × भुजा
• समकोण समद्विबाहु त्रिभुज का कर्ण = (√2) × भुजा
• समकोण समद्विबाहु त्रिभुज का क्षेत्रफल = ½ × भुजा²

Mensuration formula in Hindi | क्षेत्रमिति( फार्मूला )सूत्र  Hindi में 

3डी क्षेत्रमिति के लिए प्रश्नों का अभ्यास करें

अब जब आप सूत्रों को समझ गए हैं, तो आइए इन प्रश्नों को हल करते हैं-

1. एक पानी की टंकी है जो 300 मीटर लंबी और 200 मीटर चौड़ी है। इस टैंक से 0.3 x 0.5m 15 किलोमीटर प्रति घंटे के क्रॉस-सेक्शन के साथ पानी बहता है। घंटों में समय निर्धारित करें जिसमें जल स्तर 10 मीटर तक पहुंच जाएगा।

2. 10 सेमी के एक घन को उसकी सभी भुजाओं पर रंगना है। यदि इस घन को 1 सेमी के कई घनों में काटा जाता है, तो कितने घनों के ठीक एक फलक पर रंग होगा?

3. व्यास d के एक ठोस गोले से अधिकतम संभव आयतन का घन काट दिया जाता है। तो, वर्ग के शेष अपशिष्ट पदार्थ का आयतन क्या होगा?

4. वर्गाकार आधार वाले किसी नियमित पिरामिड के सभी 5 फलकों का क्षेत्रफल समान होता है। 5 सेमी पिरामिड की ऊंचाई है, सभी सतहों के कुल क्षेत्रफल की गणना करें।

5. त्रिज्या 6 और ऊंचाई 8cm वाले शंकु में अंकित किए जा सकने वाले घन की भुजा की विमाएँ क्या होंगी?

6. एक अर्धगोले को पिघलाकर एक शंकु के आकार में बदल दिया गया है, जिसकी आधार त्रिज्या 20 सेमी है। यदि शंकु की ऊँचाई H है, तो शंकु की त्रिज्या और ऊँचाई के बीच संबंध ज्ञात कीजिए।

7. एक धातु की गोलाकार गेंद को एक शंकु में पुनर्निर्मित किया गया है। बेल का व्यास 6 सेमी जबकि शंकु के आधार का व्यास 12 सेमी है। शंकु की ऊंचाई कितनी है?

8. एक बेलन का आयतन 1500 घन मीटर है। इसके आधार की त्रिज्या 50 मीटर है। निर्धारित करें कि सिलेंडर की ऊंचाई क्या होगी।

9. सिद्धार्थ ने अपने कमरे को पेंट कराने का फैसला किया है। उसकी दीवारों का आयाम 20m x 40m x 12m है। चित्रकारों ने रु. 20 प्रति वर्ग मीटर। सिद्धार्थ को अपने कमरे की पेंटिंग के लिए चित्रकारों को कितनी राशि देनी होगी?

10. एक लकड़ी के गोले से जिसकी त्रिज्या 25 सेमी है, 20 सेमी ऊँचाई और 40 सेमी व्यास का एक शंकु काटा गया है। बर्बाद होने वाली लकड़ी का प्रतिशत निर्धारित करें।

क्षेत्रमिति के सभी फार्मूला हिंदी | Mensuration formula in Hindi

ALL MENSURATIN FORMULA
SQUARE	Perimeter of square = 4 × a Area of the square = (side × side) = a² and side = area Area of square = × (product of diagonals) = × d2 Diagonal of square = one side × 2 = a × 2 Diagonal of the square = 2 × Area of the square
RECTANGLE	Perimeter of rectangle = 2(length + breadth) Area of rectangle = length × breadth Diagonal of rectangle =√(length² + breadth²)
TRAPEZIUM	area of trapezium = (sum of parallel sides x height) = (area of the parallelogram) = (base x corresponding height)   Perimeter, P = a + b + c + d
RHOMBUS	A + B + C + D = 360°   Area of Rhombus = × Product of both the diagonals That is, A = (d1 × d2)/2 square units Perimeter of rhombus = 4 × one side In rhombus = (AC)² + (BD)² = 4a² cyclic quadrilateral formula   A + C = 180° B + D = 180°   Area = √s(s-a) (s-b) (s – c) (s – c)] Perimeter, S = ( a + b + c + d )
POLYGON	Sum of interior angles of a quadrilateral of side n = 2(n –2) × 90° Each interior angle of a regular polygon = (n – 2) / 2 × 180° Sum of exterior angles of a polygon of n sides = 360° Sum of some interior angles of a polygon = (n – 2) × 180° Each interior angle of a rhombus of side n = [2(n – 2) × 90°] / n Perimeter of polygon = n × one side Area of regular hexagon = 6 × 3 (side)² Each exterior angle of a rhombus of side n = 360°/n Area of regular hexagon = 3√3×½ (side)² side of the rectangle = radius of the circumcircle Perimeter of regular hexagon = 6 × side Number of diagonals of a regular polygon of n sides = n(n – 3)/2
CIRCLE	Area of circle = π r² diameter of circle = 2πr Circumference of circle = 2πr circumference of circle = π d Radius of circle = Area of circle/π Area of circular ring = (R2 – r2) Perimeter of semicircle = (πr + 2 r ) Area of semicircle = 1/2πr²
CUBE	Volume of cube = side × side × side = a3 Perimeter of cube = 4 a² One edge of the surface = √ (Area of the surface / 4 ) One side of the cube = 3√Volume One side of the cube = √ (Area of the whole surface / 6 ) Total surface area of cube = 6a² Diagonal of cube = √3 × side
CUBOID	Volume of cuboid = l × b × h Perimeter of cuboid = 2(l + b) × h Total surface area of cuboid = 2(lb + bh + hl) Diagonal of cuboid = √ (l² + b² + h²) Height = Volume / (Length × Breadth) of the cuboid Cuboid Width = Volume / (Length × Height) Area of the four walls of the room = 2h ( l + b ) Area of the tank without lid = 2h ( l + b ) + lb Area of roof or floor = length × breadth
CYLINDER	Volume of cylinder = πr2h Height of cylinder = Volume / πr2 Radius of right circular cylinder =√ ( Volume /π h) Volume of metal in hollow cylinder = h (R2 – r2 ) Curved surface area of the cylinder = 2πrh Total surface area of the cylinder = 2πr ( h + r ) Height of the right circular cylinder = (Complete surface area of the cylinder / 2πr) – r Area of base of right circular cylinder = πr2
CONE	Volume of cone = 1/3 πr2h Slant height of right circular cone =√ ( h2 + r2 ) Height of cone = √ (l2 – r2 ) Radius of base of cone =√ (l2 – h2 ) Curved surface area of cone = πrl Total surface area of right circular cone = πr ( l + r ) Area of base of cone = πr2
CIRCLE	Curved surface area of the sphere = 4πr2 Volume of the sphere = 4/3 πr3 Volume of spherical shell = 4/3π ( R3 – r3 ) Total surface area of spherical shell = 4/3 π ( R2 – r2 ) The volume of the largest sphere in the cube = 1/6 a3 Surface area of the largest sphere in a cube = πa2 One side of the largest cube in the sphere = 2R / √3 Area of curved surface of the hemisphere = 2π r2 Total surface area of a hemisphere = 3 πr2 Volume of the hemisphere = 2/3πr3

FAQ 1 :मैथ्स में मेन्सुरेशन क्या है?

गणित में, क्षेत्रमिति को विभिन्न 2D और 3D ज्यामितीय आकृतियों के माप के अध्ययन के रूप में परिभाषित किया जाता है जिसमें उनके सतह क्षेत्र, आयतन आदि शामिल होते हैं।

FAQ 2 :क्षेत्रमिति और ज्यामिति में क्या अंतर है?

क्षेत्रमिति आकार के विभिन्न मापदंडों जैसे परिधि, क्षेत्र, आयतन, आदि की गणना को संदर्भित करता है, जबकि ज्यामिति विभिन्न आकृतियों के बिंदुओं और रेखाओं के गुणों और संबंधों के अध्ययन से संबंधित है।.

FAQ 3 :2डी और 3डी क्षेत्रमिति क्या हैं ?

2डी क्षेत्रमिति विभिन्न मापदंडों की गणना से संबंधित है जैसे कि वर्ग, आयत, वृत्त, त्रिकोण, आदि जैसे 2-आयामी आकृतियों के क्षेत्रफल और परिधि। 3डी क्षेत्रमिति सतह क्षेत्र, पार्श्व सतह क्षेत्र, और घन, गोले, घनाभ, शंकु, सिलेंडर, आदि जैसे 3-आयामी आंकड़ों के अध्ययन और गणना से संबंधित है।

FAQ 4 :एक वर्ग का क्षेत्रफल और परिमाप ज्ञात कीजिए जिसकी भुजा 10 सेमी है। ?

हल: दिया है: भुजा = a = 10 cm एक वर्ग का क्षेत्रफल = a2 वर्ग इकाई सूत्र में "a" के मान को रखने पर हमें प्राप्त होता है एक वर्ग का क्षेत्रफल = 102 A = 10 x 10 = 100 अत: एक वर्ग का क्षेत्रफल = 100 cm2 एक वर्ग का परिमाप = 4a इकाई P = 4 x 10 =40 अत: एक वर्ग का परिमाप = 40 सेमी.

FAQ 5 : त्रिज्या 70 सेमी और आयतन 154000 घन सेमी के वृत्ताकार आधार वाले बेलन की ऊँचाई ज्ञात कीजिए। ?

हल: दिया गया है, r= 70 cm वी = 154000 सेमी3 चूंकि सूत्र है, V = πr2h H = v/πr2 = 1543000/15400 =10 अत: बेलन की ऊँचाई 10 सेमी है।,

FAQ 6 :यदि किसी त्रिभुज की भुजाएँ 26 सेमी, 24 सेमी और 10 सेमी हैं, तो उसका क्षेत्रफल क्या है?

हल: 26 सेमी, 24 सेमी और 10 सेमी भुजाओं वाला त्रिभुज समकोण है, जहां कर्ण 26 सेमी है। त्रिभुज का क्षेत्रफल = 1/2 * 24 * 10 = 120 सेमी2

FAQ 7 :एक समलंब का क्षेत्रफल ज्ञात कीजिए जिसकी समानांतर भुजाएँ 20 सेमी और 18 सेमी लंबी हैं, और उनके बीच की दूरी 15 सेमी है।?

हल: समलम्ब चतुर्भुज का क्षेत्रफल = 1/2 (समानांतर भुजाओं का योग) * (उनके बीच लंबवत दूरी) = 1/2 (20 + 18) * (15) = 285 सेमी2

FAQ 8 :एक समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसका आधार 24 सेमी और ऊंचाई 16 सेमी है।?

हल: समांतर चतुर्भुज का क्षेत्रफल = आधार * ऊँचाई = 24 * 16 = 384 सेमी2